In this first post about the upcoming VisWeek 2010 papers, I want to talk about two papers in an area which I know a little bit about, and which I think is a very nice recent development. Back in 2006, Hamish Carr and two of his students, Brian Duffy and Barry Denby, noted one could compute histograms of scalar fields differently than the obvious way, and differently in an interesting way. Instead of counting the node or cell values, there is an equivalent integral expression in terms of a function defined on the isosurface. The original paper had a small bug in it, and in 2008 that got fixed. In parallel, Bachthaler and Weiskopf generalized the technique to multiple dimensions, which turned it into a real visualization technique. The basic idea of their Continuous Scatterplots is to think of the visualization as mapping some mass from the spatial domain to the data domain. Each point in space has a certain value, and densities of these values are different. For example, the density of data points with zero altitude is much larger than the one with an altitude of, say, ten thousand feet. The interesting derivation in their paper is the one for multidimensional datasets; it has now led to several followup papers, eg. using the same technique for parallel coordinates, and making it more efficient.
(Since these are all preprints, I will not post images of the papers; please refer to the linked files)
The first paper I want to talk about, “Discontinuities in Continuous Scatterplots” by Lehmann and Theisel, talks about a new twist on the idea of Continuous Scatterplots. One of the issues which arise when drawing these scatterplots is that the spatial domain gets mapped fairly arbitrarily to the data domain. It is sensible that one would like to have some general idea of the relation between those two domains, and one of the ways one can do that is to indicate the boundary of the spatial domain. Another interesting feature of these plots is that sometimes the spatial domain folds over itself when the mapping “changes direction” (for an appropriate definition of the term, obviously). It turns out both of these are manifestations of the differential structure of the plot breaking down; they are discontinuities. So the authors develop the math to detect these points and show how one can draw them in an NPR-like fashion. I think, personally, that the folding patterns are a more informative than the boundary ones (again, see the paper for the figures, but I’m thinking specifically about Figure 7c). All in all, nice combination of theory and pretty pictures, which is what vis research is all about :). One question I’d like to see answered is whether these extra lines help the user; since something very similar to continuous scatterplots are used extensively in transfer function widgets for volume visualization, it’d be interesting to see the relation between the boundary and fold lines and the transfer functions created by users.
The second paper I want to talk about, “On the Fractal Dimension of Isosurfaces” by Khoury and Wenger, has a more theoretical bent. One of the original reasons I became interested in the original 2006 paper of Carr, Denby and Duffy was that their argument makes it possible for us to actually do math on the histogram computations; we can compute things like the derivative of the histogram. It might also help explain a few questions we don’t quite know how to answer. In particular, Khoury and Wenger directly take on the original “mystery” of 2006’s paper, which was the observation that the observed rate of growth of isosurface statistics was much too large to be explained by what we thought was the behavior of isosurfaces inside volumes. In 2008, we noticed that scalar noise seemed to have a strong effect on these statistics, but we didn’t quite know how to analyze it directly. This analysis, I am very happy to say, is exactly what Khoury and Wenger did: they found the right way to compute the characteristics of a particular noise model which we used in 2008. With their analysis, they can explain and predict directly the impact of noise in a related statistic: the fractal dimension of a set. One interesting application of this is in noise reduction. One of the problems in denoising scalar fields is deciding when to stop: have we smoothed away all the good stuff, or have we only thrown away noise? Perhaps this framework can be used to inform the stopping time of these smoothing techniques.
One question I didn’t see answered in Khoury and Wenger’s work is a subtle point that we raised in our 2008 paper, perhaps not very clearly. Specifically, the issue is that there are many ways one can take “averages of all isosurfaces”, and unfortunately they generate different results. Counting all isosurfaces by sampling the isovalues uniformly is one possible definition, but it has the disadvantage that (for example), if one changes the scalar field by mapping all the scalars through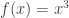 
, all the isosurfaces will be preserved, but the number you arrive at is different. This means that this number you just computed has something to do with the isosurfaces, but it also has something to do with the scalar distribution, and perhaps that’s not what is intended. I’d like to see the fractal dimension computation where the average is taken in a way that’s invariant to these mappings; would the results be different, and how so? The easiest way to do enforce this invariance is to just equalize the histogram of the scalar field before computing the statistics; in our 2008 paper we show why this is the case. If one is worried about quantization artifacts, there’s an alternative Monte Carlo integration technique as well, by uniformly sampling points in the scalar field and using their isovalues.
This is very nice work, and it shows how much there’s still out there left to understand about isosurfaces. One direct avenue for future work is to see if we can use this to understand noise in vector fields. Vector field experts might answer this question I have: what are good decompositions of vector fields in coordinate-free scalar fields? I know about the Helmholtz decomposition which works nicely in 2D, giving a potential field and a vorticity field. But in 3D it gives a scalar field and a vector potential, which does not solve the problem. However, 2D might already be a starting point.
Next up, we’ll turn to more traditional visualization topics, and in particular about evaluation of visualizations. This one paper I have in mind might be one of the best Vis papers I’ve seen in the last five years, so stay tuned!
. If you have tetrahedra, pentatopes, etc. in your mesh, they would just keep alternating signs. The Euler characteristic kind of looks like the cardinality of a set. First, it obeys the straightforward property that 
(keeping the intuition of triangle meshes: simply count up the simplices).
. This formula makes sense for finite sets (using the cartesian product), but is sort of crazy for more general spaces because it’s easy to come up with spaces of negative Euler characteristic. If you dig up the proofs for this, however, they tend to be a lot more complicated and give very little intuition. So here’s a simple proof that works for 
, that is, the degree of the monomial represents the dimension, and the coefficient represents the number of cells of that dimension. The Euler characteristic, then, is found by simply evaluating this polynomial at value 
.
. If you think about how to create the product space, you will see that you get one 
-dimensional cell for every 
-dimensional cell in 
and every 
-dimensional cell in 
. The simplest way to express this is as a product between the two polynomials! So 
, and since I hopefully convinced you that the Euler characteristic is obviously just an evaluation of 
, it is “obvious” that 
. So the “magic” comes from the rule used to create the product space. Really neat.
visualization, etc. 